Dr. J's Maths.com
Where the techniques of Maths
are explained in simple terms.
Where the techniques of Maths
are explained in simple terms.
Calculus - Differentiation - Basic techniques.
Test Yourself 1.
- Algebra & Number
- Calculus
- Financial Maths
- Functions & Quadratics
- Geometry
- Measurement
- Networks & Graphs
- Probability & Statistics
- Trigonometry
- Maths & beyond
- Index
Find the gradient function of the following functions - that is "differentiate each of the following functions" with respect to the given variable. All questions use only the direct technique as described - no special rules.
As always - your first step is to look at the structure and decide what you need to do.
| The questions below focus on the structures of: |
| 1. the basic format. |
| 2. the use of simple brackets. |
| 3. the use of the d/dx format. |
| 4. radicals. |
| 5. terms in the denominator. |
| 6. fractions with only one term in the denominator. |
| 1. Basic format. | 1. y = x3 + x
Answer.3x2 + 1. |
2. y = 3x3 + 2x2 - x - 42 | 3. y = 4x2 + 5x |
| 4. y = 3t - 5t2 | 5. y = 0.5x4 + 1.5x2 - 42 | 6. y = x2.5 |
|
| 2. Simple brackets. | 7. s = 2t2(3t + 4) | 8. m = 4n3(n5 + 3n - 1) | 9. y = 3x3(2x4 - 5x2 - x) |
| 3. Use of d/dx format. | 10. 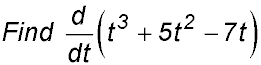
|
11. 
|
12. 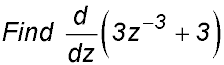
|
13. 
|
14. 
|
15. 
|
|
| 4. Radicals. | 16. |
17. 
|
18. 
|
| (see the Solutions for the answers to Q 18 - 21). | 19. |
20.  |
21. 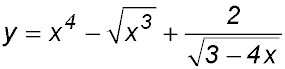 |
| 5. terms in the denominator - so the neeed to use negative signs. | 22. 
|
23. 
|
24. 
|
25. 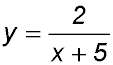
|
26. 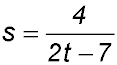
|
27. 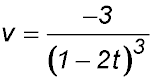
|
|
| 6. Fractions with 1 term in the denominator. | 28. 
Hint.How many terms in the denominator? ONE. So divide each term in the numerator by the term in the denominator and then differentiate normally. |
29. 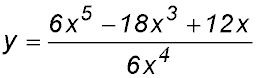
|
30. 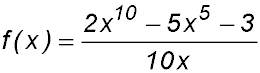 |